一、判断题1.钟面上秒针从数字6走到数字12经过的时间是30秒。（ ） 2.四边形就是指长方形、正方形、平行四边形。（ ） 3.把一个蛋糕分成5份，每份是这个蛋糕的五分之一。（ ） 4.用两根同样长的铁丝分别围一个长方形和一个正方形，正方形的周长比长方形的周长长。（ ） 5.小明有4种文具，小东有5种文具，那么他们两人一定有9种文具。（ ） 二、选择题6.数学课上，小明将被减数百位和十位上的数字互换了，结果减去263后，差是328，正确的差应该是（ ）。A. 588 B. 688 C. 65 D. 2567.下图中甲图形的周长（ ）乙图形的周长。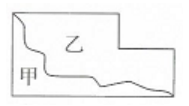 
A. 大于 B. 小于 C. 等于8.跑道长100米，同学们跑接力，每组5人，每人跑一个往返，每组要跑（ ）。
故答案为：正确。
【分析】钟面被12个数字平均分成12大格，分针走过每个大格是5分钟，分针经过几个大格，就走了几个5分钟，时针走1大格是1时，时针走1大格，分针正好走60小格，也就是60分；钟面上有60个小格，分针走1小格是1分，秒针走过每个小格是1秒，走过每个大格是5秒，走过几个大格，就是几个5秒，据此解答。
2.【答案】 错误
【考点】四边形的特点及分类
【解析】【解答】 四边形有长方形、正方形、平行四边形、梯形等，原题说法错误。
故答案为：错误。
【分析】由四条边围成的封闭图形叫四边形，常见的四边形有长方形、正方形、平行四边形、梯形，还有一般的四边形，据此判断。
3.【答案】 错误
【考点】分数单位的认识与判断
【解析】【解答】 把一个蛋糕平均分成5份，每份是这个蛋糕的五分之一，原题说法错误。
故答案为：错误。
【分析】根据分数的意义：把单位“1”平均分成若干份，表示这样的一份或者几份的数叫做分数；在分数里，中间的横线叫做分数线；分数线下面的数，叫做分母，表示把单位“1”平均分成多少份；分数线上面的数叫做分子，表示有这样的多少份，据此判断。
4.【答案】 错误
【考点】长方形的周长，正方形的周长
【解析】【解答】 用两根同样长的铁丝分别围一个长方形和一个正方形，正方形的周长等于长方形的周长，原题说法错误。
故答案为：错误。
【分析】 用两根同样长的铁丝分别围一个长方形和一个正方形，铁丝的长度是围成图形的周长，据此判断。
5.【答案】 错误
【考点】集合重叠问题
【解析】【解答】 小明有4种文具，小东有5种文具，有可能他们有重复的文具，无法确定他们一共有几种文具，原题说法错误。
故答案为：错误。
【分析】根据生活经验可知，文具的种类很多，小明与小东有可能有重复的文具，也有可能没有重复的文具，所以无法确定他们一共有几种文具，据此判断。
二、选择题
6.【答案】 B
【考点】万以内数的进位加法，万以内数的退位减法
【解析】【解答】328+263=591，那么正确的被减数是951，减数是263，差为951-263=688。
故答案为：B。
【分析】根据题意可知，先用现在的减数与差相加，得到看错的被减数，然后将看错的被减数百位和十位上的数字互换，得到正确的被减数，最后用被减数-减数=差，据此列式解答。
7.【答案】 C
【考点】周长的认识，组合图形的周长的巧算
【解析】【解答】甲图的周长=长+宽+中间的曲线部分，乙图的周长=长+宽+中间的曲线部分，甲图的周长=乙图的周长。
故答案为：C。
【分析】根据周长的定义：围成一个封闭图形一周的长度，叫图形的周长，据此分别得到甲、乙图形的周长，然后对比即可解答。
8.【答案】 B
【考点】千米与米之间的换算与比较，用连乘解决实际问题
【解析】【解答】5×2×100
=10×100
=1000（米）
=1（千米）
故答案为：B。
【分析】此题主要考查了用连乘解决问题，用每组的人数×每人跑的趟数=每组跑的总趟数，然后用每组跑的总趟数×每趟的长度=每组跑的总长度，最后将米化成千米，除以进率1000，据此解答。
9.【答案】 B
【考点】整十、整百、整千数与一位数的乘除法，三位数乘一位数的进位乘法
【解析】【解答】 计算230×7时，230的“3”与乘数7相乘得21，这里的“21”表示21个十。
故答案为：B。
【分析】 根据整数乘法计算法则：先用一个因数每一位上的数分别去乘另一个因数各个数位上的数，用因数哪一位上的数去乘，乘得的积的末尾就对齐那一位，然后把各次乘得的数加起来，据此解答。
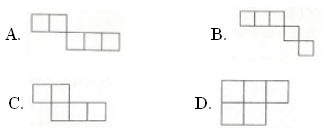
10.【答案】 B
【考点】组合图形的周长的巧算
16厘米＞14厘米＞12厘米＞10厘米，图形B的周长最长。
故答案为：B。
【分析】根据周长的定义：围成一个封闭图形一周的长度之和叫图形的周长，据此分别求出各图的周长，然后比较大小即可。
三、解决问题
11.【答案】 4；1；158
【考点】最佳方案：最省钱问题
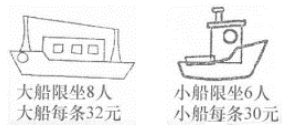
【解析】【解答】因为32÷8=4（元），30÷6=5（元），4＜5，所以尽量多租大船且不要留空位，
38÷8=4（条）……6（人）
可以租4条大船，1条小船，刚好可以坐满各条船，
需要：32×4+30
=128+30
=158（元）
故答案为：4；1；158。
【分析】根据题意可知，用每条船的价钱÷可以坐的人数=每个座位的钱数，据此分别求出大船、小船每个座位的价钱，然后对比可知，大船每个座位的钱数少些，所以多租大船而且要不留空位，据此解答。
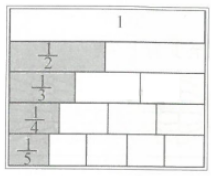
【分析】（1）根据分数的意义：把单位“1”平均分成若干份，表示这样的一份或者几份的数叫做分数；在分数里，中间的横线叫做分数线；分数线下面的数，叫做分母，表示把单位“1”平均分成多少份；分数线上面的数叫做分子，表示有这样的多少份，据此找出分数墙里的分数；比较同分子分数的大小，看分母，分母越大，这个分数越小；
（2）要求1里面有几个分数单位，看分母，分母是几，就有几个分数单位。
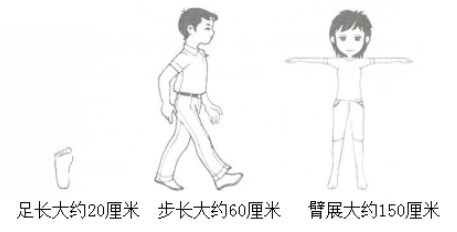
13.【答案】 （1）9
（2）解：步长，测量过程：先确定起点，作上记号，然后围绕篮球场走一圈，记下步数，然后用步数×60=篮球场一圈的长度。
【考点】长度的估算，物体长度的测量与计算
【解析】【解答】（1） 如聪聪的指甲盖宽约为1厘米，他正在用指甲盖量下图中铅笔的长度。我估计这支铅笔的长度大约是9厘米。
【分析】（1）观察可知，铅笔的长度大约有9个指甲盖的宽度，据此估算；
（2）根据题意可知，用步长来测量即可。
14.【答案】 解：2个大瓶=3个中瓶，则4个大瓶=6个中瓶=11个小瓶
8个大瓶=22个小瓶
答：买8个大瓶的钱可以买22个小瓶。
【考点】代换问题
【解析】【分析】此题主要考查了代换问题，根据条件“ 买4个中瓶的钱可以买2个大瓶和1个中瓶 ”可知，买2个大瓶的钱数等于买3个中瓶的钱数，由此可得，买4个大瓶的钱数等于买6个中瓶的价钱，根据条件“ 买11个小瓶的钱可以买6个中瓶 ”可以得到，买4个大瓶的钱数等于买11个小瓶的钱数，那么买8个大瓶的钱数就等于买11×2=22个小瓶的钱数，据此解答。
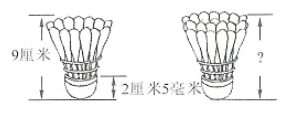
15.【答案】 （1）解： 90+25=115（毫来）
答：这时高度是115毫米。
（2）解：90+25×8=290（毫米）
答：这个包装桶的长度至少为290毫米。
（3）把3个羽毛球叠在一起，有多高？；把5个羽毛球叠在一起，有多高？
【考点】米、分米、厘米、毫米之间的换算与比较，1000以内数的四则混合运算
【解析】【分析】（1）观察图可知， 2个羽毛球紧紧地叠在一起， 这时的高度=一个羽毛球的高度+一个底座的长度，据此列式解答；
（2） 观察图可知，把9个羽毛球叠好装在圆包装桶里，这个包装桶的长度=一个羽毛球的高度+一个底座的长度×8，据此列式解答；
（3）根据题中的信息，可以提出问题1：把3个羽毛球叠在一起，有多高？问题2：把5个羽毛球叠在一起，有多高？据此解答。
16.【答案】 解：60÷2÷（5+1）=5（厘米）
5×5=25（厘米）
25×4=100（厘米）
答：正方形的周长为100厘米。
【考点】长方形的周长，正方形的周长
【解析】【分析】根据题意可知，把一个正方形平均分成5个相等的长方形，则长方形的长是宽的5倍，根据条件“每一长方形周长为60厘米”，用长方形的周长÷2÷（5+1）=长方形的宽，再用长方形的宽×5=长方形的长，长方形的长为正方形的边长，要求正方形的周长，用公式：正方形的周长=边长×4，据此列式解答。
17.【答案】 解：4+1=5
40÷5=8（岁）
8×4=32（岁）
答：小明今年8岁，妈妈今年32岁。
【考点】和倍问题
【解析】【分析】此题主要考查了和倍应用题，和倍应用题的公式是：两数和÷两数的倍数和=小数，小数×倍数=大数，如果把妈妈的年龄和小明的年龄看成一个整体，则妈妈占其中的4份，小明占1份，则两人的年龄和刚好平均分成5份，用年龄和÷（4+1）=小明的年龄，然后用小明的年龄×4=妈妈的年龄，据此列式解答。
18.【答案】 （1）15；18
（2）10；11
（3）13；16
【考点】数列中的规律
【解析】【解答】（1）因为0+3=3，3+3=6，6+3=9，9+3=12，所以12+3=15，15+3=18。
（2）因为1+1=2，2+2=4，4+1=5，5+2=7，7+1=8，所以8+2=10，10+1=11。
（3）因为1+2=3，3+3=6，6+2=8，8+3=11，所以11+2=13，13+3=16。
故答案为：（1）15；18；（2）10；11；（3）13；16。
【分析】（1）观察数列可得规律：前一个数+3=后一个相邻的数，据此规律解答；
（2）观察数列可得规律：第一个数+1=第二个数，第二个数+2=第三个数，第三个数+1=第四个数，第四个数+2=第五个数，据此规律解答；
（3）观察数列可得规律：第一个数+2=第二个数，第二个数+3=第三个数，第三个数+2=第四个数，第四个数+3=第五个数，据此规律解答。
19.【答案】 解：42-22=20（千克）
20×2=40（千克）
答：这筐苹果原来有40千克。
【考点】100以内数乘法与加减法的混合运算
【解析】【分析】根据条件，先求出半筐苹果的质量，用一筐苹果连筐的质量-半筐苹果加筐的质量=半筐苹果的质量，然后用半筐苹果的质量×2=这筐苹果的质量，据此列式解答。
20.【答案】 解：4×5=20（个）
20+10=30（个）
90里有3个30，每个茶杯3元，
3×4=12（元）
答：茶杯3元，保温杯12元。
【考点】代换问题，倍的应用
【解析】【分析】根据条件“ 每个保温杯是每个茶杯价格的4倍 ”可知，5个保温杯的价钱相当于5×4=20个茶杯的价钱，然后用20个茶杯的价钱+10个茶杯的价钱=90，求出一个茶杯的价钱，最后用每个茶杯的价钱×4=每个保温杯的价钱，据此列式解答。
21.【答案】 解：36÷2=18（本）
18+5=23（本）
18-5=13（本）
答：原来小红有23本，小华有13本。
【考点】整数平均分及其应用，100以内数的四则混合运算
【解析】【分析】根据题意可知，用小红和小华的故事书总本数÷2=现在每人的故事书本数，然后用现在每人的故事书本数+5=原来小红的故事书本数，现在每人的故事书本数-5=原来小华的故事书本数，据此列式解答。
22.【答案】 60；31
【考点】100以内数的四则混合运算
【解析】【解答】 个位上的0丢掉的加数是：
（91-37 ）÷（10-1）
=54÷9
=6
正确的那个加数是：6×10=60，
另一个加数是：91-60=31。
故答案为：60；31。
【分析】此题主要考查了差倍问题的应用，根据题意可知，两个算式的差，就是加数的差，因为一个加数去掉的个位上是0，所以原来正确的加数是后来去掉0的加数的10倍，用两个算式的差÷相差的倍数=原来的加数，最后用和-一个加数=另一个加数，据此列式解答。
23.【答案】 解：2×3=6÷1=4+7-5（答案不唯一）
【考点】横式数字谜
【解析】【分析】此题主要考查了横式数字谜，先确定相等的数是几，然后选择合适的运算使等式成立，注意： 每个数字只能用一次，据此解答。
